Does Changing Speed of Light Violate Energy Conservation?

The Problem

One problem for young-earth creationists (those claiming that God created the universe only thousands of years ago, rather than billions of years ago) has been the apparent great age of distant galaxies.

Decay of the speed of light

Several theories have been advanced to deal with the above problem, including the idea that the speed of light, known as c, was greater in the past than it is now. Therefore, according to this idea, the faster light in the ancient universe reached earth sooner than astronomers suspect because they assume a much slower speed for light. That is to say, it did not take so long (billions of years, for example) for light from stars and galaxies to reach the earth, and, consequently, they need not be so old (billions of years, for example). The idea that the speed of light was greater in the past, and that it has decayed or slowed down to what is now currently observed, is commonly referred to as CDK, for C (speed of light) decay (which sounds like “Dee-Kay” or “DK”). In this article, “CDK” will be used to refer to the decay of the speed of light.

Energy conservation issue

There have been several arguments given both in support of and also denying the possibility of CDK. One argument is that the decay of the speed of light was not possible, because CDK would violate the law of the conservation of energy (really, conservation of mass-energy). 1

The argument against CDK, using violation of energy conservation, goes as follows. If the speed of light was faster in the past, then by the equation E = mc² energy would have been greater in the past since increasing c in this equation results in increasing E, or energy. But, E should remain constant in order to obey the law of conservation of energy. So CDK would violate energy conservation, and thus CDK could not have happened.

However, this argument is not valid. In this article we shall examine this commonly asserted reason that CDK could not be true and show why it is not valid, with a mathematical derivation that E, energy, remains constant when c changes for some CDK models.

The result will be shown that energy conservation is not violated by CDK. (Other arguments, such as whether relativity is violated by CDK, will not be dealt with in this article due to space limits.)

Assumptions

In this section we shall examine the assumptions of both the energy-conservation violation argument against CDK and the assumptions used to refute that argument.

Assumptions for violation of energy conservation by CDK

We will show in this paper that the law of conservation of energy is not violated by CDK! How so?

The argument that energy conservation is violated by CDK assumes that one factor, m, in the equation E = mc² is constant and does not change when c changes. We shall show that this assumption is false.

Below is a mathematical derivation showing that m would indeed change when c changes, and what is more, that m will change in exactly such a manner as to cancel out the effect of increasing c on energy, E. Thus, the derivation shows that energy conservation would not be violated by CDK.

Assumptions for mathematical disproof of violation of energy conservation by CDK

Assumptions 1, 2, and 3: accepted conventional formulae

One might ask regarding the assumptions used in the mathematical derivation in this article, “What are the assumptions going into this math?” Are those assumptions really valid; or are they assumed, merely to make the derivation work, without any evidence from observational data?

Let’s look at the assumptions for the following mathematical derivation— the first three of which are conventional and widely accepted— and also look at the observational evidence for the other assumptions.

First, we will tacitly accept that the following three key equations for this proof are valid:

$$E = mc^2$$

$$E = hf$$

$$f = c/w$$

where E is energy, f is frequency, w is wavelength, c is the speed of light, and h is Planck’s constant.

We note that these equations, though listed as assumptions, are part of accepted conventional physics and can be found in many physics textbooks.

The final two assumptions are also listed as assumptions, but there is observational data supporting both of them.

Assumption 4: hc is constant

In addition to the above, we shall also assume that Planck’s constant (h) is inversely proportional to the speed of light (c). In other words, the product hc is a constant, or h = k/c, where k is some constant.

Evidence

The product of h and c, or hc, has been measured to be constant to within parts per million. 2 3 4 5 6

Also, while c has been measured as decreasing over time, h has been measured as increasing over time.

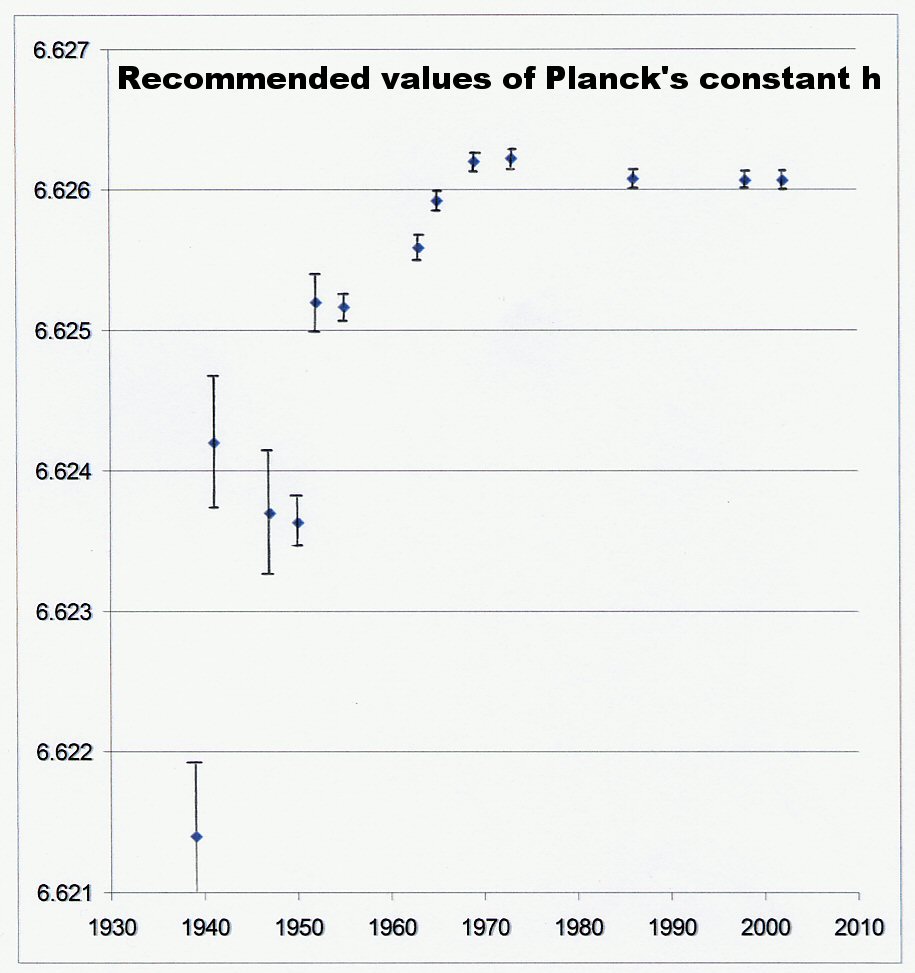
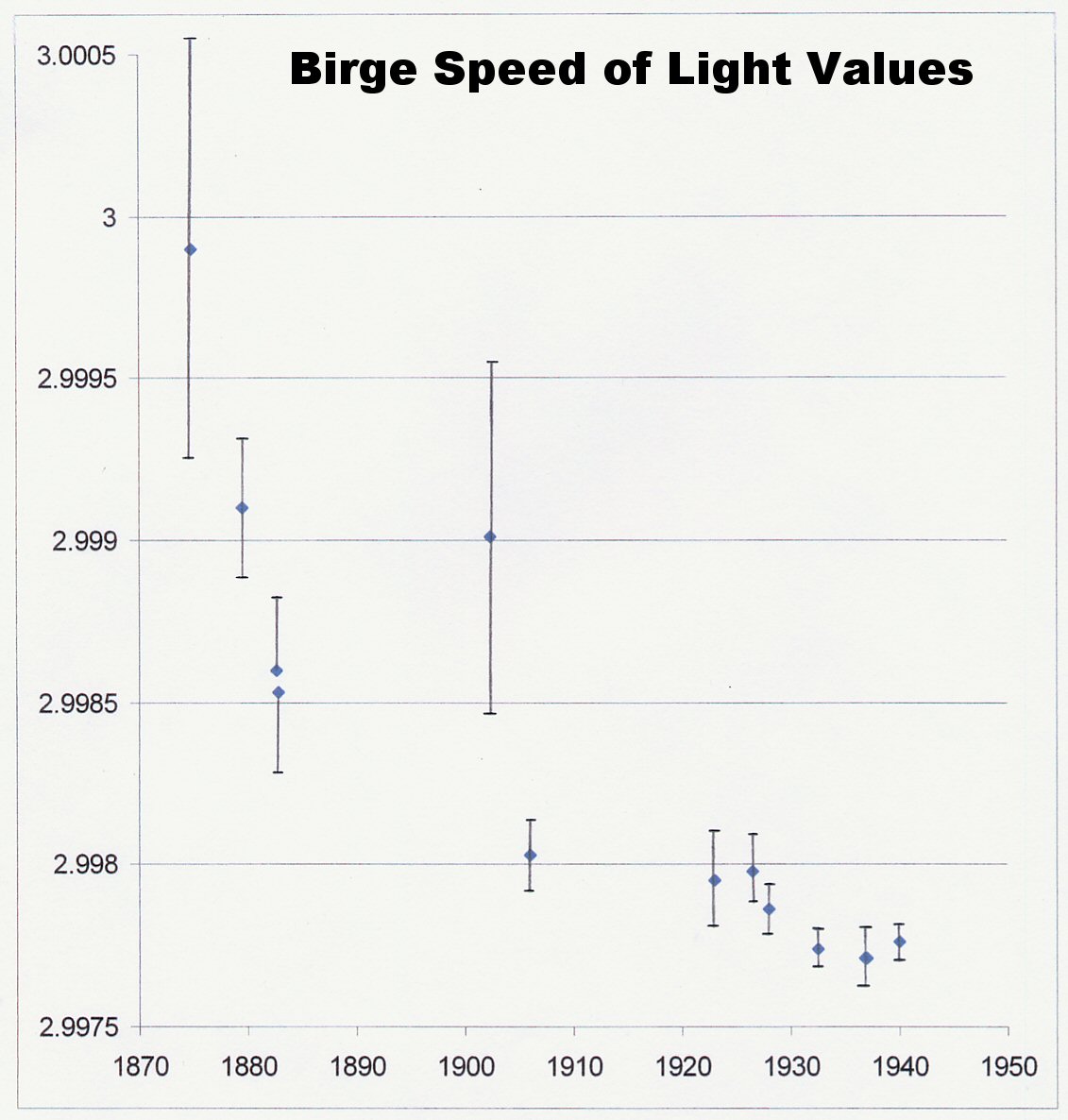
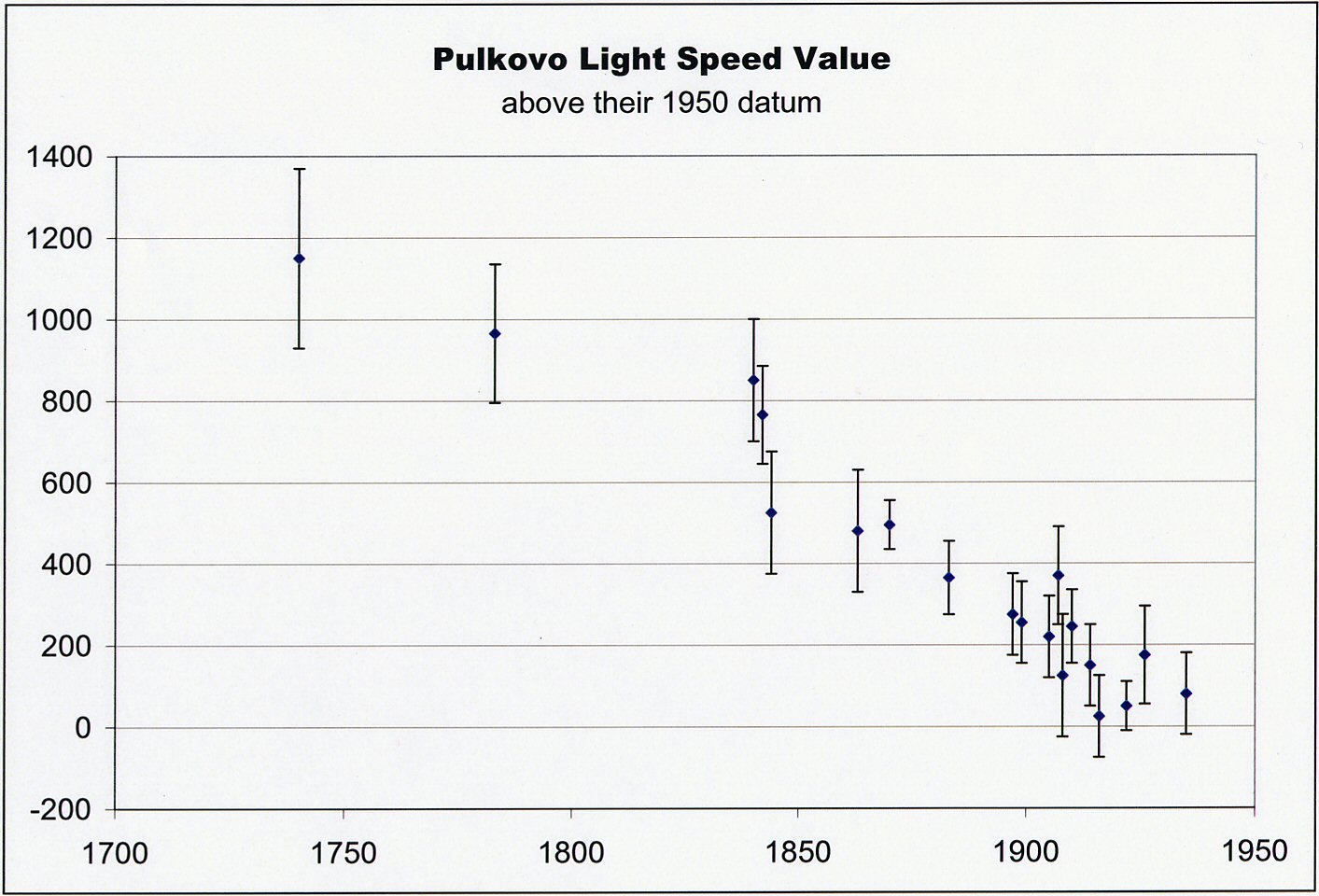
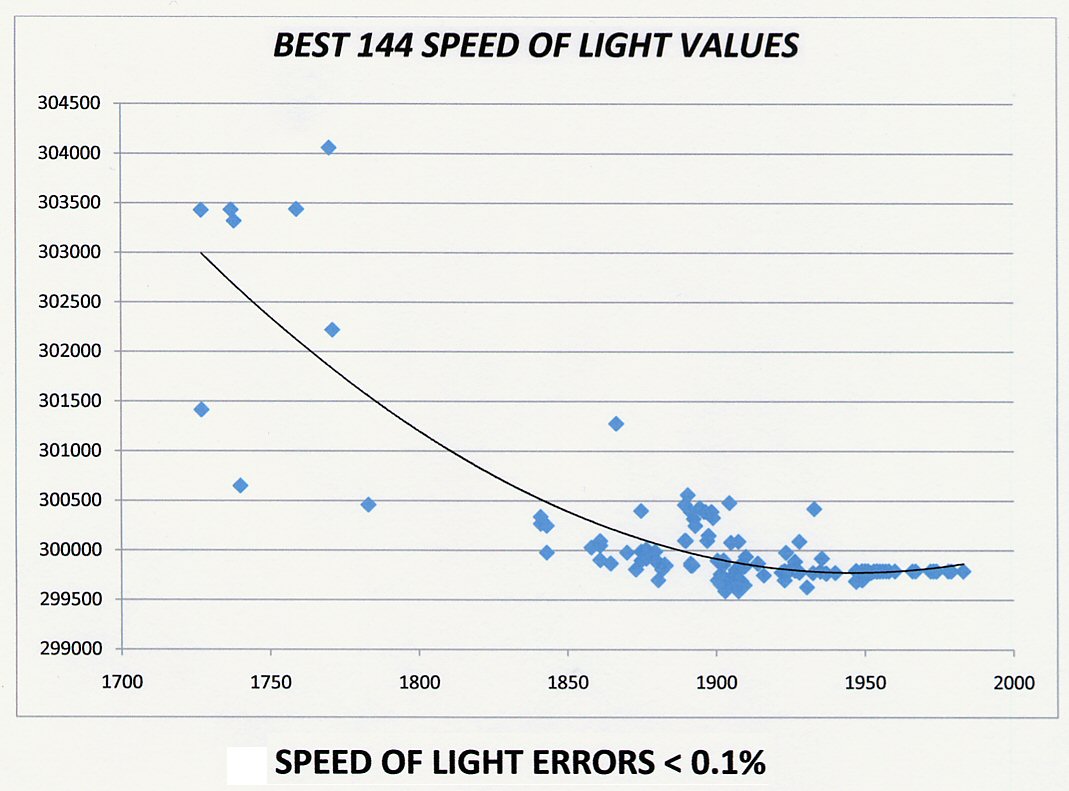
Note the upward trend in the measured values of Planck’s constant (h) in Figure 1 and the downward trend in the measured values of the speed of light (c) in Figure 2. The date range is not identical, but there is some small overlap. The trends show that while h was measured as increasing, c was measured to be decreasing. Figure 4 shows more recent values for the speed of light, also going back further in time, past 1750. The downward trend in c is also apparent there. Figure 3 shows measurements from the same location using the same instruments, which should remove instrumental error; yet still we see the downward trend of the measured values of the speed of light.

So, if h is shown to be increasing while c is decreasing, and their product has been found to be constant, 2 3 4 5 6  then the only obvious conclusion is that they (h and c) are inversely proportional.

We note that we saw above that this assumption is supported by evidence from measured data.

The fine structure constant

Other evidence for h being inversely proportional to c is found in measurements of the fine structure constant, which shows very little change (stable to one part in a million), 7 8 in spite of the measured changes in both h and c. The fine structure constant is composite, and its formula includes both h and c. The measured changes in h and c, and the measured extremely small variation in the fine structure constant, can be explained by, and provide support for, h and c being inversely proportional.

The formula for the fine structure constant is below:

\[ \alpha=\frac{e^2}{\epsilon}\frac{1}{2hc} \] where \( \epsilon \) is the electric permittivity of free space, and \( e \) is the charge of the electron. (The further explanation of \( \epsilon \) and the other components of the fine structure constant is outside the scope of this article.) It can be noted that if h and c are both changing, while \( \alpha \) is not changing, this suggests that h and c are inversely proportional. 

Assumption 5: constant wavelength of light from galaxies

The other assumption is that the wavelength of photons of light, that travel from distant galaxies to arrive and be observed (detected) on earth, is also constant.

One reason often cited for rejecting this assumption is the conventional red shift explanations. These explain red shift by the stretching of the wavelength of light due to the expansion of the universe, and/or by the Doppler effect, which would likewise stretch out the waves of light. However, both these explanations of red shift have problems. One problem is that different red shifts have been measured for connected objects. Connected objects are obviously in close proximity and should have the same or similar red shifts. Measured different red shifts for these objects is a problem. Another observation that conventional red shift interpretations fail to explain is the apparent quantization of the red shift data.

However, these explanations are not the only explanations for red shift data! Another explanation of the red shift that avoids these problems is simple; it is merely that the light was originally redder when it was originally emitted from the distant galaxies, and that each photon (or wave) of light maintained that same (redder) wavelength while continuing on its journey to earth. According to other, more conventional, explanations of red shift, the wavelength of light changes because of the expansion of space or because of the Doppler effect. Narlikar and Arp showed that the universe need not be expanding in order to avoid collapse. 9 So it is not necessary to assume expanding space, nor the conventional explanations for red shift. Therefore, we shall assume the red shift occurs at the time of emission, rather than during transit.

Observations About Assumptions

We note that all of the assumptions made in the refutation of the violation of CDK are well accepted in conventional physics, and/or are supported by observational evidence, and/or are supported by calculations, and/or solve other problems. There are good scientific reasons for these assumptions, not just ad-hoc reasons to prove Genesis.

On the other hand, we note that there is a single assumption, that of mass being constant while c changes in the equation E = mc², on which hinges the claim that CDK violates energy conservation! Regarding the idea that mass can never change, note that mass does indeed change according to Einstein’s theory of special relativity (where m is mass and v is velocity):

\[ m_{new}=\frac{m_{old}}{\sqrt{(1-v^2/c^2)}} \]So, this assumption of unchanging mass might indeed be questioned since mass does indeed change per special relativity. (The assumptions for the proof below seem better supported than the assumption of constant mass, that the proof below disproves.)

Briefly, the first three assumptions are well established laws of physics. The fourth assumption is verified by observation. The fifth and last assumption explains red shift and resolves some mysteries associated with red shift. Also, the fifth assumption is part of at least one CDK model; and if we change the model that we are evaluating, then we are not evaluating that model, but a different one.

Now that we have elaborated the assumptions, we are ready for the proof.

The Proof

Proof that E = mc² is not violated by a changing c (by CDK)

We will use the following symbols in the proof below:

E is energy

m is mass

c is the speed of light

f is the frequency of light

w is the wavelength of light

h is Planck’s constant

k is a proportionality constant

K is another constant

The key equations for this proof are the three below:

\[E=mc^2 \tag 1 \]

\[E=hf \tag 2 \]

\[f=\frac{c}{w} \tag 3 \]

The above are basic accepted formulas of physics.

We will also use the following two assertions of the CDK model (which are supported by observational data, as pointed out above):

1. hc is constant (based on observational measurements).
2. The wavelength of light does not change while traveling from the source galaxy (or star) to earth (that is based on an interpretation of red shift data that avoids problems that other interpretations have and that also explains observed red shift quantization).

From the observed data and from the model, h is inversely proportional to c:

\[h=\frac{k}{c} \tag 4 \]

Also, from assumption 5, w is constant:

\[ w = constant \tag 5 \]

Thus, equating the right sides of equations 1 and 2, we get

$$mc^2=hf \tag 6 $$

and substituting equation 3 into equation 6, we get

$$mc^{2}=hf=h(\frac{c}{w}) \tag 7 $$

Now, canceling out the common factor c from both left and right sides, we get

$$mc=\frac{h}{w} \tag 8 $$

Substituting equation 4 into equation 8, we get

$$mc=\frac{h}{w}=\frac{(k/c)}{w} \tag 9 $$

Rearranging the right side, we get

$$mc=\frac{k}{cw} \tag {10} $$

Dividing both sides by c, we get

$$m=\frac{k}{c^{2}w} \tag {11} $$

Note that k is a constant, and the light wavelength in this model is constant (per Assumption 5), so w (light wavelength) is also a constant. 

We now can rearrange the equation a bit, to isolate those constants (k and w) into a separate factor, \((k/w)\).

$$m=(\frac{k}{w})(\frac{1}{c^{2}}) \tag {12} $$

Since both k and w are constant, diving one by the other is also a constant, or k/w is a constant, which we shall name capital K. Then we can replace the fraction consisting of both these constants k and w, \((k/w)\), by the constant capital K, by simply setting \(K = k/w\). We then get

$$m=K(\frac{1}{c^{2}}) \tag {13} $$

or, that mass is inversely proportional to the speed of light squared!

This means that as c increases, m decreases, and vice versa.

We can plug equation 13 into equation 1 now:

$$E=mc^2=[K(\frac{1}{c^{2}})]c^{2} \tag {14} $$

Simplifying,

$$E=K(\frac{c^{2}}{c^{2}}) \tag {15} $$

And we see that \( c^2 \) cancels out:

$$E=K(1) \tag {16} $$

or, simply 

$$E=K \tag {17} $$

We see that E is the constant K, and c squared cancels out; so no matter how c changes, E still remains the constant, K!

Therefore, since energy E does not change when c changes (CDK), conservation of energy is maintained and is not violated. Thus, we have shown that CDK does not violate the conservation of energy.

Relevance & Summary

“So what?” we might ask. What is the relevance of this proof? This derivation, by showing that CDK does not violate energy conservation, removes one obstacle to the possibility of CDK. Since CDK could allow light from distant stars to reach earth in less time than the current estimates of billions of years, those stars might possibly be younger than supposed, and this in turn removes one obstacle to reconciling the apparent long ages for distant stars with a young universe, thereby removing one argument against young-earth creation.

There are other beliefs/opinions regarding CDK, which are beyond the scope of this article. However, by examining this derivation, we can see that one assumption about CDK has fallen; perhaps other beliefs, which may be only assumptions (or possibly false assumptions), ought to be examined more closely or re-examined too, to see if they might be false also.

• 1Since matter and energy are interconvertible, this energy conservation law has been reframed as the law of conservation of mass and energy. Energy and mass are related by the famous equation governing the transformation of matter into energy.
• 2 a b Setterfield BJ, Setterfield HJ (2013) Cosmology and the Zero Point Energy. Natural Philosophy Alliance Monograph Series, 53. http://www.barrysetterfield.org/GSRdvds.html#cosmology Accessed 2021 Jan 14
• 3 a b Bahcall JN, Salpeter EE (1965) Astrophys. J. 142:1677–1681
• 4 a b Baum WA, Florentin-Nielsen R (1976) Astrophys. J. 209:319–329
• 5 a b Solheim JE, Barnes III TG, Smith HJ (1976) Astrophys. J. 209:330–334
• 6 a b Noerdlinger PD (1973) Phys. Rev. Lett. 30:761–762
• 7Cowie LL, Songaila A (2004) Nature 428:132
• 8Bouchendira R, Cladé P, Guellati-Khélifa S, Nez F, Biraben F (2011) New determination of the fine structure constant and test of the quantum electrodynamics. Physical Review Letters 106(8):080801 https://hal.archives-ouvertes.fr/hal-00547525/file/MesureAlpha2010.pdf Accessed 2021 Jan 14
• 9Narlikar J, Arp H (1993) Flat spacetime cosmology: A unified framework for extragalactic redshifts. Astrophysical J. 405:51–56